info

方針

  • コーダーにとってわかりやすい
  • なるべく愚直な方法で
  • 計算時間とメモリ容量を守る

AtCoder ABC099 を Python3 で解く

ちょっと順番が前後しますが順に過去に向かっても掘り下げていこうかと思います
公式の解説はこちら
https://img.atcoder.jp/abc099/editorial.pdf

A. ABD

数字までprint しなきゃいけないかと思ってたら違いました。 問題文良く読めという話

  • 1, 2… 999 のとき “ABC”
  • 1000, 1001…のとき “ABD”

を出力すれば良いので解法は正直に考えれば
input() を int に変換して大小を比較する方法でしょうか。
str のまま受け取って len(str) で比較しても良いですけど……

Accepted Code [A. ABD]

1
2
3
4
5
6
7
input_num = int(input())

if input_num < 1000:
    print("ABC")

else:
    print("ABD")

B. Stone Monument

与えられた2つの「雪より出てる部分の高さ」から、雪の積もった高さが等しいことを利用すると、
2つの塔の高さの差がわかります。すると、例えば
1+2+3+4 1+2+3+4+5 となる2つの塔の差が5 になる というように例を考えていけば、
(低い方の塔の高さ) = 1+2+...+(塔の高さの差 - 1)
となります

さて、塔の高さが求まればあとは簡単な話で
(雪の深さ) + (塔の雪から出ている部分) = (塔の高さ)
を低い方か高い方、どちらかの塔に対して計算すれば良いです。今回は低い方で考えています

Accepted Code [B. Stone Monument]

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
def delta2lower_height(arg_num):
    height = 0
    for i in range(1, arg_num):
        height += i
    return height


# main
input_line = input().split()

higher_margin = int(input_line[0])
lower_margin = int(input_line[1])

delta = higher_margin - lower_margin

lower_height = delta2lower_height(delta)
snow_height = lower_height - lower_margin

print(str(snow_height))

C. Strange Bank

こんな銀行預けたくない さて、考えていきましょう……
6^n 円引き出す時を考えると、6^n 円 を引き出す動作 * 6回は、明らかに
6*6^n = 6^(n+1) となるため、6^(n+1) 円 1回 を引き出す動作と金額が等しくなり、
5回分を無駄に使うことになってしまいます。よって、
6^n 円を引き出す動作はすべての n∈(自然数) に対して5回までと制限することができます。
同様のことは9^n 円についても言えます (8回まで)

また、問題条件より額が100000円を下回ることから、

  • 6^7 = 279936 円
  • 9^6 = 531441 円
    これ以上の引き出しはできないことになります。

よって、引き出しの動作としては以下のものが挙げられます

  • 1 円
  • 6^1, 6^2, 6^3, 6^4, 6^5, 6^6 円
  • 9^1, 9^2, 9^3, 9^4, 9^5 円

引き出し全体としては、これらの引き出しが0回以上組み合わされると考えられます。
ところで、6^n 円の引き出し系統の回数が定められた時、
残る動作は 9^n 円の引き出しと1円の引き出しのため、最適な引き出し方法が一意に定まります。

よって、6^1… 6^6 円 について 0回以上5回以下 = 6 * 6 * 6 パターンについて調べる方法で
十分に短い時間で全ての(最適な)組み合わせについて調べることができます。

Accepted Code [C. Strange Bank]

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
input_num = int(input())

combinations = [(pow1, pow2, pow3, pow4, pow5, pow6)
                for pow1 in range(0, 6)
                for pow2 in range(0, 6)
                for pow3 in range(0, 6)
                for pow4 in range(0, 6)
                for pow5 in range(0, 6)
                for pow6 in range(0, 6)]

num_withdraw_list = []
for combination in combinations:
    pow1, pow2, pow3, pow4, pow5, pow6 = combination
    withdraw6 = 6 ** 1 * pow1 + 6 ** 2 * pow2 + \
                6 ** 3 * pow3 + 6 ** 4 * pow4 + \
                6 ** 5 * pow5 + 6 ** 6 * pow6

    if withdraw6 > input_num:
        continue
    else:
        rest = input_num - withdraw6
        num_withdraw = sum(combination)
        for i in reversed(range(1, 6)):
            withdraw_i = rest // 9 ** i
            rest -= 9 ** i * withdraw_i
            num_withdraw += withdraw_i
        num_withdraw += rest
        num_withdraw_list.append(num_withdraw)

print(str(min(num_withdraw_list)))

D. Good Grid

Accepted Code [D. Good Grid]

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
import copy


input_line = input().split()
grid_size = int(input_line[0])
num_color = int(input_line[1])

differential_cost = {}
for color_from in range(1, num_color + 1):
    input_line = input().split()
    for color_to in range(1, num_color + 1):
        differential_cost[(color_from, color_to)] = int(input_line[color_to-1])

color_map = {}
for x in range(1, grid_size + 1):
    input_line = input().split()
    for y in range(1, grid_size + 1):
        color_map[(x, y)] = int(input_line[y-1])

current_color_dict = {}
for color in range(1, num_color+1):
    current_color_dict[color] = 0

current_color_mod0 = copy.deepcopy(current_color_dict)
current_color_mod1 = copy.deepcopy(current_color_dict)
current_color_mod2 = copy.deepcopy(current_color_dict)

for index, color in color_map.items():
    x, y = index
    if (x + y) % 3 == 0:
        current_color_mod0[color] += 1
    elif (x + y) % 3 == 1:
        current_color_mod1[color] += 1
    elif (x + y) % 3 == 2:
        current_color_mod2[color] += 1

combinations = [(color_mod0, color_mod1, color_mod2)
                for color_mod0 in range(1, num_color+1)
                for color_mod1 in range(1, num_color+1)
                for color_mod2 in range(1, num_color+1)]

cost_list = []
for combination in combinations:
    color_mod0, color_mod1, color_mod2 = combination
    if color_mod0 == color_mod1 or color_mod0 == color_mod2 or color_mod1 == color_mod2:
        continue

    cost = 0
    for color_from in range(1, num_color+1):
        cost += differential_cost[(color_from, color_mod0)] * current_color_mod0[color_from]
        cost += differential_cost[(color_from, color_mod1)] * current_color_mod1[color_from]
        cost += differential_cost[(color_from, color_mod2)] * current_color_mod2[color_from]

    cost_list.append(cost)

print(str(min(cost_list)))

ABC099 の軌跡

ABC099 の提出記録です。実行時間や使用メモリもわかります。銀行恨むぞ
https://beta.atcoder.jp/contests/abc099/submissions?f.Task=&f.Language=&f.Status=&f.User=nuekodory

AtCoder

AtCoder ABC101 / ARC 099 を Python3 で解く

【公式リンク】図表とざっくりとした解説はこちらからどうぞ。
https://img.atcoder.jp/arc099/editorial.pdf

A. Eating Symbols Easy

高橋君が命令文をもぐもぐ食べます。

  • 最初は0
  • “+” で1増加

  • “-“ で1減少

    と単純なので、言葉の通りに実行してみましょう。

    Accepted Code [A. Eating Symbols Easy]:

1
2
3
4
5
6
7
8
9
10
orders = input()

number = 0
for order in orders:
    if order == '+':
        number += 1
    else:    # order == '-'
        number -= 1

print(str(number))

B. Digit Sums (Easy)

まずこの問題のいうS(n) を返す関数を作ってみましょう。
各桁の数字を足し合わせて返せばいいわけですね。

ところで “各桁の数字を1つずつ切り出す” 方法にはいくつかあります。
一番pythonic なのはこんなのですかね：

https://stackoverflow.com/questions/14939953/sum-the-digits-of-a-number-python

1
2
3
4
5
6
7
8
# written by Uli Köhler on stackoverflow.com

def sum_digits(n):
    s = 0
    while n:
        s += n % 10
        n //= 10
    return s

もちろんこれでも良いのですが、iterable でくるくる回す方が簡単に思いつく(気がする)ので、
文字列str(number) を for で回して1文字ずつ文字(chr) を切り出します。
切り出した文字はint() で囲ってやると数字に戻ります。

1
2
3
4
5
6
7
def sum_of_digits(arg: int) -> int:
    arg_str = str(arg)
    sum_digits = 0
    for char in arg_str:
        sum_digits += int(char)

    return sum_digits

さて、あとは”割り切れる”かどうかを判定すれば良いです。これは剰余(a % b)が0であることと等価です。
また、条件より入力Nは正の整数なのでゼロ除算は考えなくて良いです。

Accepted Code [B. Digit Sums (Easy)]:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
def sum_of_digits(arg: int) -> int:
    arg_str = str(arg)
    sum_digits = 0
    for char in arg_str:
        sum_digits += int(char)

    return sum_digits


# main
input_num = int(input())

if input_num % sum_of_digits(input_num) == 0:
    print("Yes")
else:
    print("No")

C. Minimization

さて公式の解説にもある通り、数列中の最小値が1であることから、
何回動作を繰り返しても数列の要素の最小値は1です。

よって全ての数字を揃えた時、必ず1に揃うことになります。
(わからなかったら手を動かして実際に動作を紙に書いて実行してみましょう)

さて、全て1に揃えればいいと気づいたところで、再び動作をよく観察すると、
1回の動作につき “1になる要素数” が最大で K-1 個できるのがわかります。
右にずらしたり左にずらしたりして試行してみると、最善の動作1回に対して
常にK-1 個の要素が1になるとわかります

最小値に揃える連続する要素の数K 試行回数 T に対し、要素が1に等しい要素数 E とすると、
最善の動作を繰り返したとき E = 1 + T * (K-1) ただしE<=N

よって、 N =< 1 + T * (K-1) になるTを求めれば良いとわかります。
数列の並びが入力されますが捨てて良いです。

Accepted Code [C. Minimization]

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
input_line = input().split()

num_array = int(input_line[0])
num_equal = int(input_line[1])

input_line = input() # 無視

equalized = 1
i = 0
while equalized < num_array:
    equalized += (num_equal - 1)
    # print(i, equalized)
    i += 1

print(str(i))

D. Sunuke Numbers

……とりあえずグラフでも描いて考えてみましょうか！(なげやり)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
import matplotlib.pyplot as plt


def sunuke_sum(arg: str) -> int:
    sum_digit = 0
    for char in arg:
        sum_digit += int(char)
    return sum_digit


sunuke_list = []
for i in range(1, 1000):
    sunuke_list.append(i / sunuke_sum(str(i)))

plt.plot(sunuke_list)
plt.ylabel("number/sunuke(number)")
plt.show()

するとこんな感じで出てきます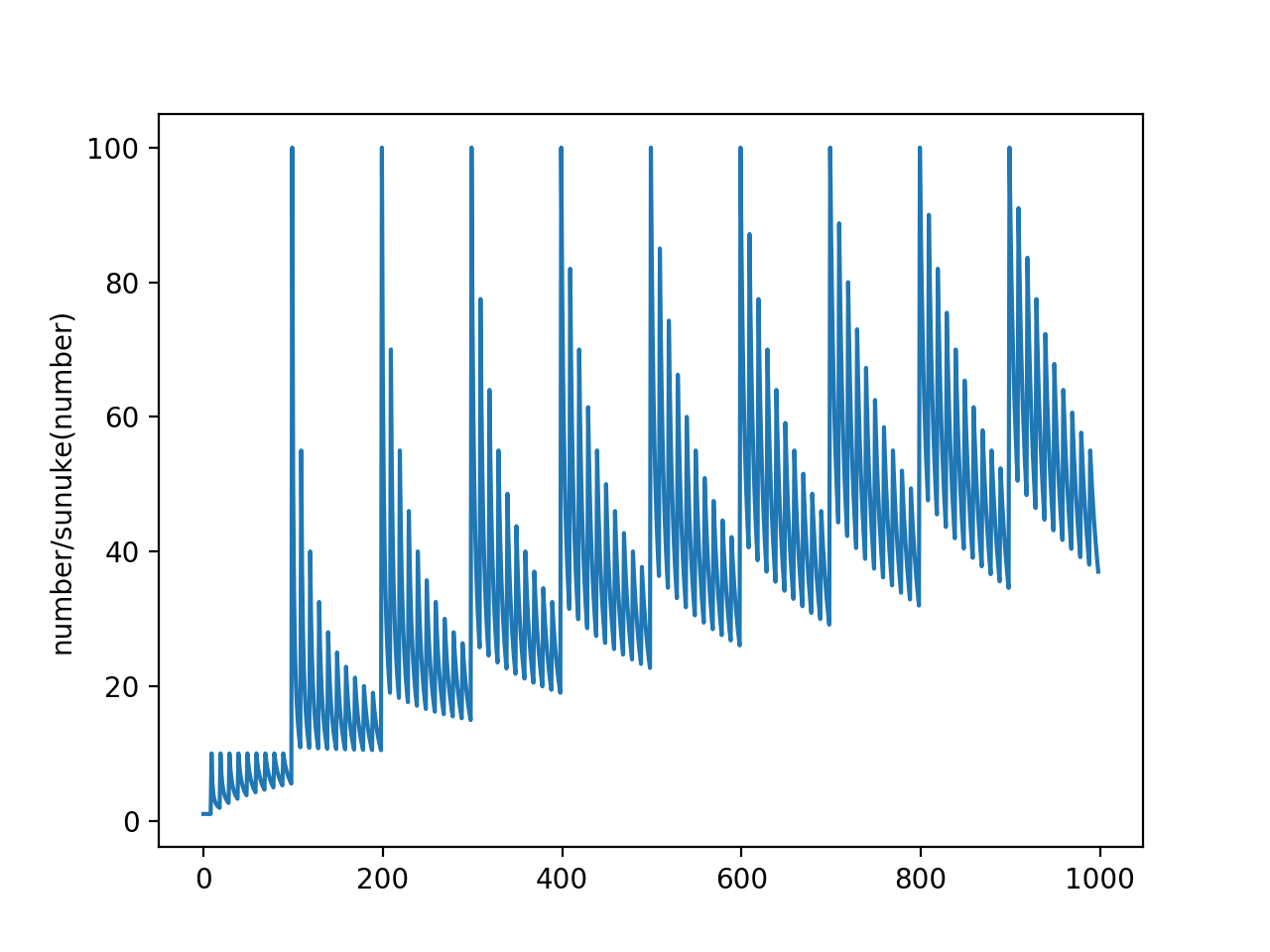

グラフパッとみた感じ、
1, 2, 3, 4, 5, 6, 7, 8, 9, 19, 29, 39, 49, 59, 69, 79, 89, 99, 199, 299, 399…

…499, 599, 699, 799, 899, 999, 1999, 2999, 3999…

って見えますね！見えますよね！残念でした！そうじゃないんです

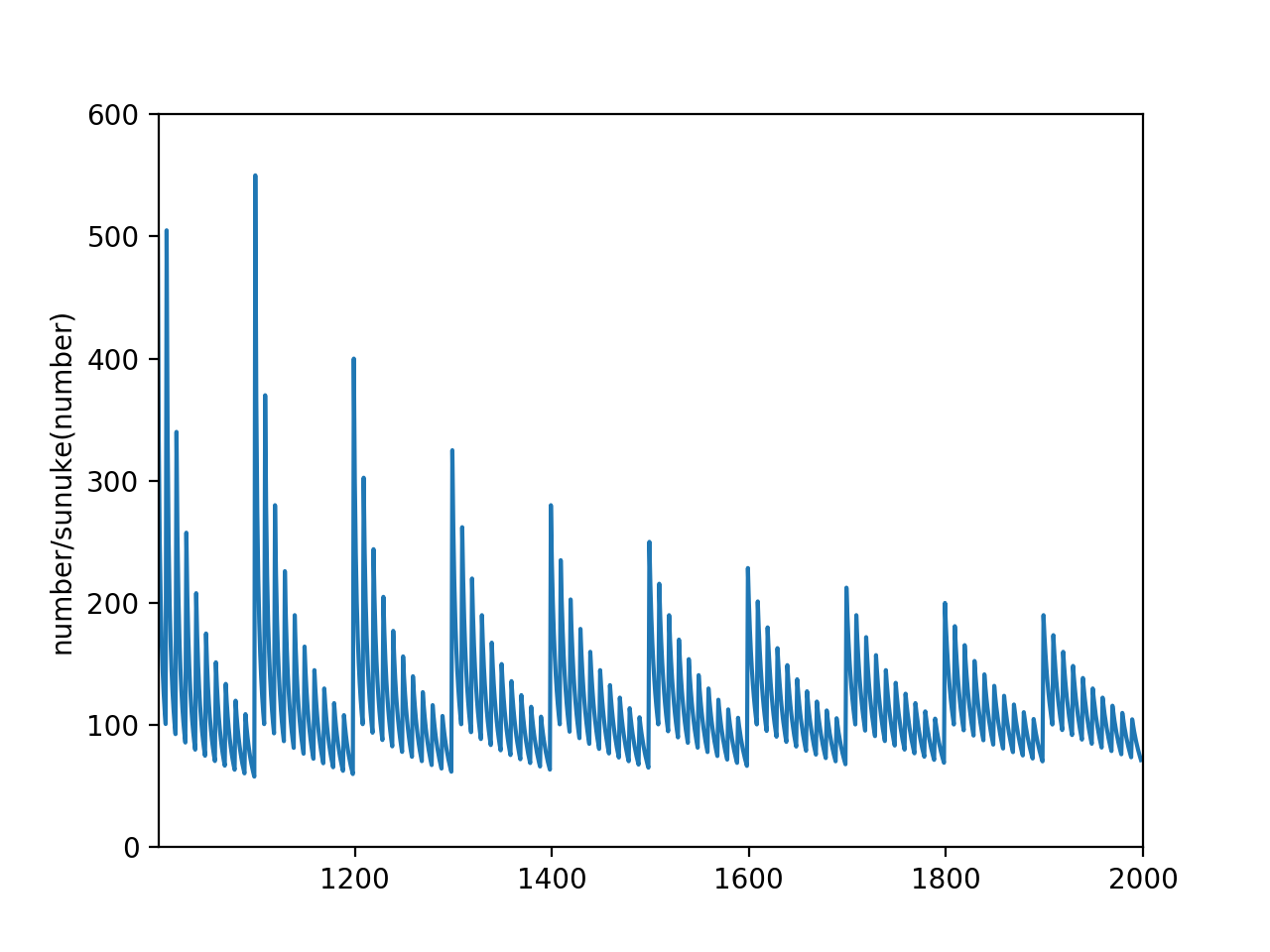
この通り、 1099, 1199, 1299, 1399… も「すぬけ値」なんですね、不可解

ところで、ランダムな数字を考えてみます(ここで爽健美茶のJANコードが登場)

4902102119450

さて、この数字から n/S(n) について考えてみると、

1
2
  4899999999999  <    4902102119450
S(4899999999999) >= S(4902102119450)

よって明らかに、
(4899999999999 / S(4899999999999) < 4902102119450 / S(4902102119450)

となる数4899999999999が存在します。

これの存在条件について考えてみると、

  • 全部で3桁以上の数
  • 上位から2桁目の数が1から9
  • 上位から3桁目以降に9以外の数が含まれる

となりますので、すぬけ数の候補は全体からこれを除いたものになります。よって

  • 1から109
  • N * (10 ** D) + (10 ** D - 1) ただし 1 <= N <= 99, 1 <= D <= 14

がすぬけ数の候補です。 (厳密にはこの中には上の条件を 満たす ものがありますが、計算しても差し支えないので計算します)

これら候補の数は限られているので、これに対して n/S(n) を算出し比較します。
便宜のため、10 ** 15 - 1 = 999999999999999 はすぬけ数であるとします。

{すぬけ数の候補: n/S(n)} となる辞書 sunuke_dict を作成し、大きい数から比較して
n/S(n) が小さいもので更新された時、このn をすぬけ数としてsunuke_list に追加します。
するとsunuke_list にすぬけ数が大きなものから順に列挙されるので、順序を逆にしてから先頭から取り出していけば答えになります。

Accepted Code [D. Sunuke Numbers]

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
def sunuke_sum(arg):
    sum_digit = 0
    for char in arg:
        sum_digit += int(char)
    return sum_digit


input_num = int(input())

sunuke_dict = {}

min_sunuke_div = 10 ** 20
for d in reversed(range(1, 16)):
    for n in reversed(range(10, 1000)):
        i = n * (10 ** d) + (10 ** d - 1)
        sunuke_div = i / sunuke_sum(str(i))
        sunuke_dict[i] = sunuke_div

for i in reversed(range(1, 110)):
    sunuke_div = i / sunuke_sum(str(i))
    sunuke_dict[i] = sunuke_div

sunuke_sorted = sorted(sunuke_dict.items())
sunuke_list = []

for value, div_value in reversed(sunuke_sorted):
    if min_sunuke_div >= div_value:
        sunuke_list.append(value)
        min_sunuke_div = div_value

sunuke_list.reverse()

for i in range(0, input_num):
    print(str(sunuke_list[i]))

E. Independence

ちょっと考えつかなかった。解説をよく読んでやっと理解できました……
さて、条件をよく読んでみると、「高」群、「橋」群の二つについて(以下 T, H とします)

  • 群を形成するすべての要素が道で繋がる = 結合している
  • 異なる群の間の道路については考えなくて良い
    となっています。(ここで止まった)

さて、ここで群を形成するための作業を

  • 群の要素間はすべて結合している
  • 群をまたぐ結合については除去する

という作業に置き換えてみると、これについての補グラフを考えると、

  • 群の要素間は結合がない
  • 群をまたぐ結合を足して、すべての要素間に結合があるようにする

となります。よって、

  • まず補グラフをとる
  • 群の要素間の結合を調べる
  • たがいに結合のない群の振り分けを考える

という動作を行えば良いことになります。
「たがいに結合のない群の振り分け」を考える時、グラフを連結成分分解
(つまり孤 isolated である集団ごとに分ける)すれば良く、

都市についてこれを求めてみます

1
2
3
4
5
6
7
8
9
10
11
12
road_dict = {1: [2, 4], 2: [1], 4:[1]} # 道の結合を示す
classified = []
all_cities = set(range(0, num_cities))

for city in range(0, num_cities):
    class_list_city_in = []
    class_list_checked = []
    if city in road_dict.keys():
        tagged = set(road_dict[city])
        graphed = all_cities - tagged
    else:
        graphed = all_cities

ARC099 の軌跡

ARC099 の提出記録です。実行時間や使用メモリもわかります。まあよくやったよ、うん
https://beta.atcoder.jp/contests/arc099/submissions?f.Task=&f.Language=&f.Status=&f.User=nuekodory

AtCoder

AtCoder ABC100 を Python3 で解く

図表とざっくりとした解説はこちらからどうぞ。
https://img.atcoder.jp/abc100/editorial.pdf

A. Happy Birthday!

図をよーく見れば、1人が9切れ以上取ることができないことが分かります。
隣接しない = 最低でも1つ間隔を開けなければならない
ということは、8切れ取った時1つ間隔で取ることになりこれが最大です。

全部で16個から8個ずつ取っても問題ないので、全体のケーキの残りについては考える必要がなく、1人最大8切れを守れば良いことになります。
(マイナスの入力は条件から存在しません)

よって、A, B が8以下であることが Yay! の条件ですので、

1
2
3
4
if A <= 8 and B <= 8:
    print("Yay!")
else:
    print(":(")

となるように設計すれば良いことになります。

Accepted Code [A. Happy Birthday!]:

1
2
3
4
5
6
7
8
9
input_line = input().split()

cake_a = int(input_line[0])
cake_b = int(input_line[1])

if cake_a > 8 or cake_b > 8:
    print(":(")
else:
    print("Yay!")

B. Ringo’s Favorite Numbers

色々な解法がありますが、ここでは D = 0 or 1 or 2 ということを利用して解きます(場合分け)

D == 0

“100でちょうど0回割り切れる” == “100で割り切れない”
と考えると解けるかと思います。
コードにすると

1
2
if number % 100 != 0:
    do

ということですね。

ここで N < 100 であれば単純に答えが N で終わりなのですが、
N <= 100 なので N == 100 について分ける必要があります。

愚直に N == 100 を場合分けしても良いですし、
100の倍数について無視してカウントするようにしても良いです(今回はこちらを採用)

D == 1

“100でちょうど1回割り切れる” == “100で割り切れて、10000で割り切れない”
よってD == 0 の時と同様に N == 100 についてのみ場合分けをするか、
10000の倍数を無視してカウントするようにすれば良いです(今回はこちらを採用)

D == 2

“100でちょうど2回割り切れる” == “10000で割り切れて、1000000で割り切れない”
よってD == 0, 1 の時と同様に N == 100 についてのみ場合分けをするか、
1000000の倍数を無視してカウントするようにすれば良いです(今回はこちらを採用)

Accepted Code [B. Ringo’s Favorite Numbers]:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
input_line = input().split()
num_divide = int(input_line[0])
smallest_of = int(input_line[1])

if num_divide == 0:
    counter = 0
    current_num = 0
    while counter < smallest_of:
        current_num += 1
        if current_num % 100 == 0:
            continue
        else:
            counter += 1

elif num_divide == 1:
    counter = 0
    current_num = 0
    while counter < smallest_of:
        current_num += 100
        if current_num % 10000 != 0 and current_num % 1000000 != 0:
            counter += 1

else:               # num_divide == 2
    counter = 0
    current_num = 0
    while counter < smallest_of:
        current_num += 10000
        if current_num % 1000000 != 0:
            counter += 1

print(str(current_num))

C. *3 or /2

“3倍する” or “2で割り切る” の操作をするのですが、

“3倍する” のはまあ何回でもできますよね。

というわけでネックになるのは “2で割り切る” ことです。
“2で割り切る” 動作は数列に対して 1回の操作で1つ以上適用しなければならないので、
1回の操作で1つを “2で割り切る” と考えます。

するとこの問題は “2で何回割り切れるか” という問題になりますので、
数列のそれぞれの数について “2で何回割り切れるか” を調べます。
いくつか方法はありますが、2進法に変換して0が続く桁数を調べるのが良いでしょう(多分)

Accepted Code [C. *3 or /2]

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
array_length = int(input())
input_line = input().split()

array_int = list(map(int, input_line))
array_bin = list(map(bin, array_int))
array_bin_str = list(map(str, array_bin))

array_dividable = []

for i in range(0, array_length):
    if array_int[i] == 0:
        array_dividable.append(0)
    else:
        target_line = array_bin_str[i]
        count_dividable = 0
        for j in range(1, len(target_line)):
            target_char = target_line[-j]
            if target_char == '1':
                break
            elif target_char == 'b':
                break
            else:
                count_dividable += 1

        array_dividable.append(count_dividable)

if sum(array_dividable) == 0:
    print("0")
else:
    print(str(sum(array_dividable)))

D. Patisserie ABC

全ての場合についてスコアを出そうとすると、ケーキ1000個から500個を取り出すときに計算量が最大で、このとき

C(1000, 500) = 2.702882409E+299

よってこんなんでfor を回すと帰ってこない(計算が終了しない)ので別の方法を考えます。

ところで、スコアは絶対値を採用するわけですが、
絶対値というのは max(number, -number) と等価です。

よってこの場合、単純にスコアを足していったあとのことを考えると、

「綺麗さ」「おいしさ」「人気度」の数値が beauty, yummy, popular だったとして

1
2
3
4
5
6
7
8
+ beauty + yummy + popular
+ beauty + yummy - popular
+ beauty - yummy + popular
- beauty + yummy + popular
- beauty - yummy + popular
+ beauty - yummy - popular
- beauty + yummy - popular
- beauty - yummy - popular

の8パターンのうち、最大のものが

1
abs(beauty) + abs(yummy) + abs(popular)

と等しいとわかります。

すると、絶対値で考えなくても単純に足していって最後にmaxを出せば良いことがわかります。

さて、ここまできたところでもう一度上の8例について見てみます。

+ beauty - yummy + popular で考えてみましょう。

これを最大化させるためには + beauty - yummy + popular を各ケーキに対して算出し、大きいものから順番にケーキの個数だけ取れば良いことに気がつくでしょうか。

すると8パターン全てに対して同じことが言えるのですから、これを計算してmax を取ればスコアが最大であると言えます。

Accepted Code [D. Patisserie ABC]

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
input_line = input().split()
total_cake = int(input_line[0])
select_cake = int(input_line[1])

cake_scores = []

for i in range(0, total_cake):
    input_line = input().split()
    beauty = int(input_line[0])
    yummy = int(input_line[1])
    popular = int(input_line[2])

    cake_scores.append((beauty, yummy, popular))

# + beauty + yummy + popular score_p_p_p
# + beauty + yummy - popular score_p_p_n
# + beauty - yummy + popular score_p_n_p
# - beauty + yummy + popular score_n_p_p
# - beauty - yummy + popular score_n_n_p
# + beauty - yummy - popular score_p_n_n
# - beauty + yummy - popular score_n_p_n
# - beauty - yummy - popular score_n_n_n

scores_p_p_p = []
scores_p_p_n = []
scores_p_n_p = []
scores_n_p_p = []
scores_n_n_p = []
scores_p_n_n = []
scores_n_p_n = []
scores_n_n_n = []

for i in range(0, total_cake):
    beauty, yummy, popular = cake_scores[i]
    scores_p_p_p.append(beauty + yummy + popular)
    scores_p_p_n.append(beauty + yummy - popular)
    scores_p_n_p.append(beauty - yummy + popular)
    scores_n_p_p.append(-beauty + yummy + popular)
    scores_n_n_p.append(-beauty - yummy + popular)
    scores_p_n_n.append(beauty - yummy - popular)
    scores_n_p_n.append(-beauty + yummy - popular)
    scores_n_n_n.append(-beauty - yummy - popular)

scores_p_p_p.sort(reverse=True)
scores_p_p_n.sort(reverse=True)
scores_p_n_p.sort(reverse=True)
scores_n_p_p.sort(reverse=True)
scores_n_n_p.sort(reverse=True)
scores_p_n_n.sort(reverse=True)
scores_n_p_n.sort(reverse=True)
scores_n_n_n.sort(reverse=True)

score_p_p_p = sum(scores_p_p_p[0:select_cake])
score_p_p_n = sum(scores_p_p_n[0:select_cake])
score_p_n_p = sum(scores_p_n_p[0:select_cake])
score_n_p_p = sum(scores_n_p_p[0:select_cake])
score_n_n_p = sum(scores_n_n_p[0:select_cake])
score_p_n_n = sum(scores_p_n_n[0:select_cake])
score_n_p_n = sum(scores_n_p_n[0:select_cake])
score_n_n_n = sum(scores_n_n_n[0:select_cake])

print(str(max(score_p_p_p, score_p_p_n, score_p_n_p, score_n_p_p,
              score_n_n_p, score_p_n_n, score_n_p_n, score_n_n_n)))

ABC100 の軌跡

ABC100 の提出記録です。実行時間や使用メモリもわかります
https://beta.atcoder.jp/contests/abc100/submissions?f.Task=&f.Language=&f.Status=&f.User=nuekodory