AtCoder

AtCoder ABC101 / ARC 099 を Python3 で解く

【公式リンク】図表とざっくりとした解説はこちらからどうぞ。
https://img.atcoder.jp/arc099/editorial.pdf

A. Eating Symbols Easy

高橋君が命令文をもぐもぐ食べます。

  • 最初は0
  • “+” で1増加

  • “-“ で1減少

    と単純なので、言葉の通りに実行してみましょう。

    Accepted Code [A. Eating Symbols Easy]:

1
2
3
4
5
6
7
8
9
10
orders = input()

number = 0
for order in orders:
    if order == '+':
        number += 1
    else:    # order == '-'
        number -= 1

print(str(number))

B. Digit Sums (Easy)

まずこの問題のいうS(n) を返す関数を作ってみましょう。
各桁の数字を足し合わせて返せばいいわけですね。

ところで “各桁の数字を1つずつ切り出す” 方法にはいくつかあります。
一番pythonic なのはこんなのですかね：

https://stackoverflow.com/questions/14939953/sum-the-digits-of-a-number-python

1
2
3
4
5
6
7
8
# written by Uli Köhler on stackoverflow.com

def sum_digits(n):
    s = 0
    while n:
        s += n % 10
        n //= 10
    return s

もちろんこれでも良いのですが、iterable でくるくる回す方が簡単に思いつく(気がする)ので、
文字列str(number) を for で回して1文字ずつ文字(chr) を切り出します。
切り出した文字はint() で囲ってやると数字に戻ります。

1
2
3
4
5
6
7
def sum_of_digits(arg: int) -> int:
    arg_str = str(arg)
    sum_digits = 0
    for char in arg_str:
        sum_digits += int(char)

    return sum_digits

さて、あとは”割り切れる”かどうかを判定すれば良いです。これは剰余(a % b)が0であることと等価です。
また、条件より入力Nは正の整数なのでゼロ除算は考えなくて良いです。

Accepted Code [B. Digit Sums (Easy)]:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
def sum_of_digits(arg: int) -> int:
    arg_str = str(arg)
    sum_digits = 0
    for char in arg_str:
        sum_digits += int(char)

    return sum_digits


# main
input_num = int(input())

if input_num % sum_of_digits(input_num) == 0:
    print("Yes")
else:
    print("No")

C. Minimization

さて公式の解説にもある通り、数列中の最小値が1であることから、
何回動作を繰り返しても数列の要素の最小値は1です。

よって全ての数字を揃えた時、必ず1に揃うことになります。
(わからなかったら手を動かして実際に動作を紙に書いて実行してみましょう)

さて、全て1に揃えればいいと気づいたところで、再び動作をよく観察すると、
1回の動作につき “1になる要素数” が最大で K-1 個できるのがわかります。
右にずらしたり左にずらしたりして試行してみると、最善の動作1回に対して
常にK-1 個の要素が1になるとわかります

最小値に揃える連続する要素の数K 試行回数 T に対し、要素が1に等しい要素数 E とすると、
最善の動作を繰り返したとき E = 1 + T * (K-1) ただしE<=N

よって、 N =< 1 + T * (K-1) になるTを求めれば良いとわかります。
数列の並びが入力されますが捨てて良いです。

Accepted Code [C. Minimization]

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
input_line = input().split()

num_array = int(input_line[0])
num_equal = int(input_line[1])

input_line = input() # 無視

equalized = 1
i = 0
while equalized < num_array:
    equalized += (num_equal - 1)
    # print(i, equalized)
    i += 1

print(str(i))

D. Sunuke Numbers

……とりあえずグラフでも描いて考えてみましょうか！(なげやり)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
import matplotlib.pyplot as plt


def sunuke_sum(arg: str) -> int:
    sum_digit = 0
    for char in arg:
        sum_digit += int(char)
    return sum_digit


sunuke_list = []
for i in range(1, 1000):
    sunuke_list.append(i / sunuke_sum(str(i)))

plt.plot(sunuke_list)
plt.ylabel("number/sunuke(number)")
plt.show()

するとこんな感じで出てきます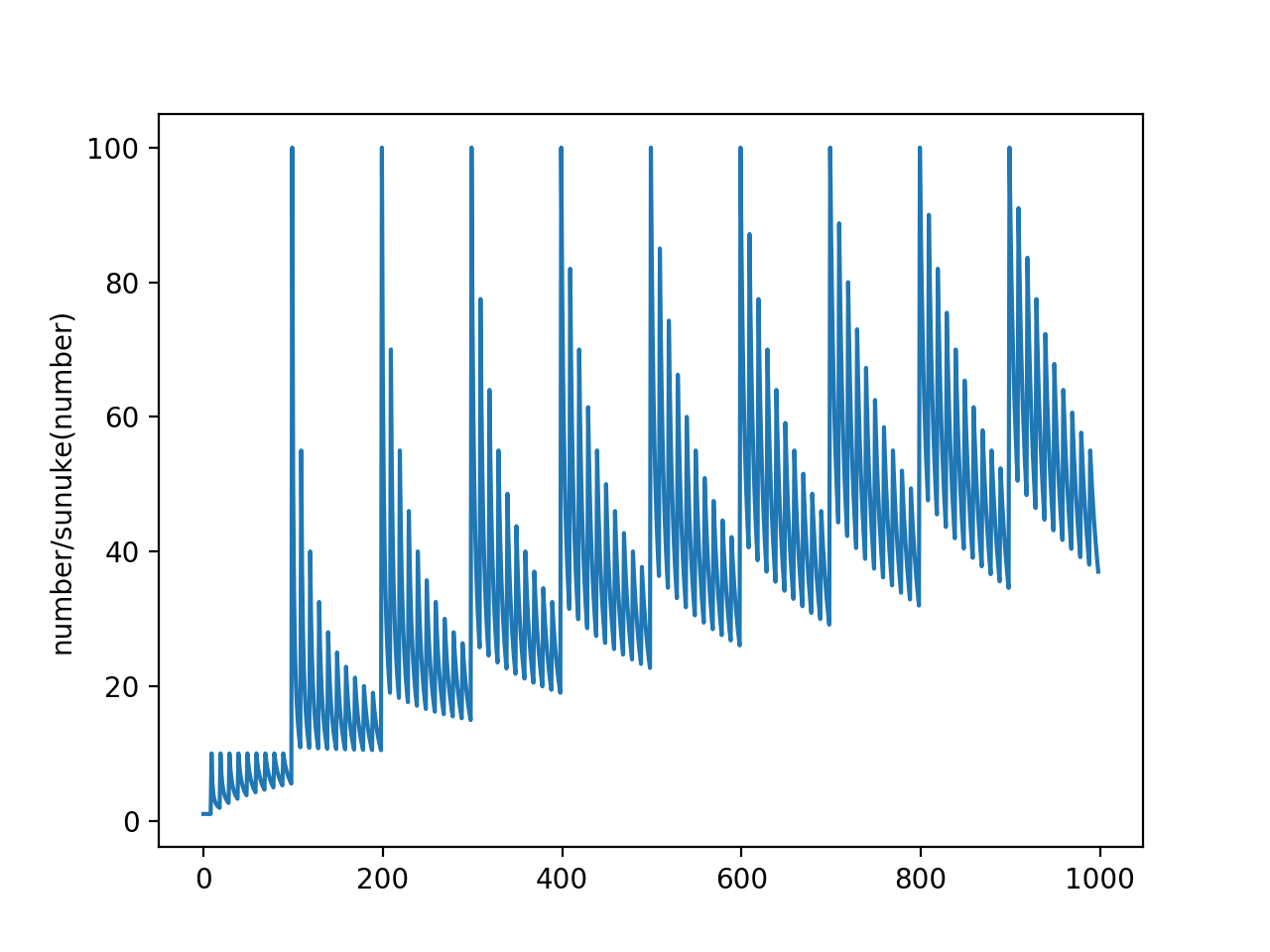

グラフパッとみた感じ、
1, 2, 3, 4, 5, 6, 7, 8, 9, 19, 29, 39, 49, 59, 69, 79, 89, 99, 199, 299, 399…

…499, 599, 699, 799, 899, 999, 1999, 2999, 3999…

って見えますね！見えますよね！残念でした！そうじゃないんです

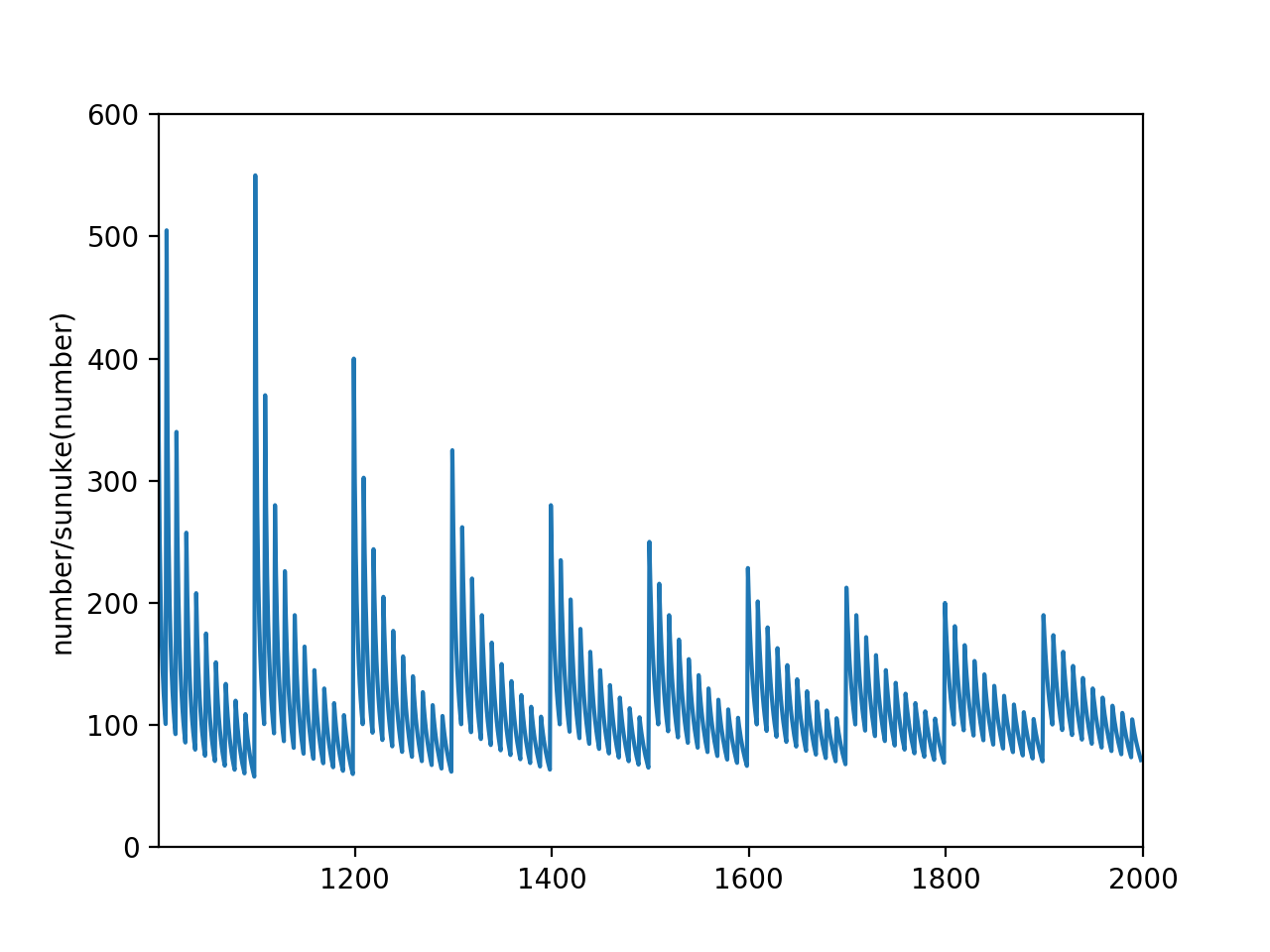
この通り、 1099, 1199, 1299, 1399… も「すぬけ値」なんですね、不可解

ところで、ランダムな数字を考えてみます(ここで爽健美茶のJANコードが登場)

4902102119450

さて、この数字から n/S(n) について考えてみると、

1
2
  4899999999999  <    4902102119450
S(4899999999999) >= S(4902102119450)

よって明らかに、
(4899999999999 / S(4899999999999) < 4902102119450 / S(4902102119450)

となる数4899999999999が存在します。

これの存在条件について考えてみると、

  • 全部で3桁以上の数
  • 上位から2桁目の数が1から9
  • 上位から3桁目以降に9以外の数が含まれる

となりますので、すぬけ数の候補は全体からこれを除いたものになります。よって

  • 1から109
  • N * (10 ** D) + (10 ** D - 1) ただし 1 <= N <= 99, 1 <= D <= 14

がすぬけ数の候補です。 (厳密にはこの中には上の条件を 満たす ものがありますが、計算しても差し支えないので計算します)

これら候補の数は限られているので、これに対して n/S(n) を算出し比較します。
便宜のため、10 ** 15 - 1 = 999999999999999 はすぬけ数であるとします。

{すぬけ数の候補: n/S(n)} となる辞書 sunuke_dict を作成し、大きい数から比較して
n/S(n) が小さいもので更新された時、このn をすぬけ数としてsunuke_list に追加します。
するとsunuke_list にすぬけ数が大きなものから順に列挙されるので、順序を逆にしてから先頭から取り出していけば答えになります。

Accepted Code [D. Sunuke Numbers]

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
def sunuke_sum(arg):
    sum_digit = 0
    for char in arg:
        sum_digit += int(char)
    return sum_digit


input_num = int(input())

sunuke_dict = {}

min_sunuke_div = 10 ** 20
for d in reversed(range(1, 16)):
    for n in reversed(range(10, 1000)):
        i = n * (10 ** d) + (10 ** d - 1)
        sunuke_div = i / sunuke_sum(str(i))
        sunuke_dict[i] = sunuke_div

for i in reversed(range(1, 110)):
    sunuke_div = i / sunuke_sum(str(i))
    sunuke_dict[i] = sunuke_div

sunuke_sorted = sorted(sunuke_dict.items())
sunuke_list = []

for value, div_value in reversed(sunuke_sorted):
    if min_sunuke_div >= div_value:
        sunuke_list.append(value)
        min_sunuke_div = div_value

sunuke_list.reverse()

for i in range(0, input_num):
    print(str(sunuke_list[i]))

E. Independence

ちょっと考えつかなかった。解説をよく読んでやっと理解できました……
さて、条件をよく読んでみると、「高」群、「橋」群の二つについて(以下 T, H とします)

  • 群を形成するすべての要素が道で繋がる = 結合している
  • 異なる群の間の道路については考えなくて良い
    となっています。(ここで止まった)

さて、ここで群を形成するための作業を

  • 群の要素間はすべて結合している
  • 群をまたぐ結合については除去する

という作業に置き換えてみると、これについての補グラフを考えると、

  • 群の要素間は結合がない
  • 群をまたぐ結合を足して、すべての要素間に結合があるようにする

となります。よって、

  • まず補グラフをとる
  • 群の要素間の結合を調べる
  • たがいに結合のない群の振り分けを考える

という動作を行えば良いことになります。
「たがいに結合のない群の振り分け」を考える時、グラフを連結成分分解
(つまり孤 isolated である集団ごとに分ける)すれば良く、

都市についてこれを求めてみます

1
2
3
4
5
6
7
8
9
10
11
12
road_dict = {1: [2, 4], 2: [1], 4:[1]} # 道の結合を示す
classified = []
all_cities = set(range(0, num_cities))

for city in range(0, num_cities):
    class_list_city_in = []
    class_list_checked = []
    if city in road_dict.keys():
        tagged = set(road_dict[city])
        graphed = all_cities - tagged
    else:
        graphed = all_cities

ARC099 の軌跡

ARC099 の提出記録です。実行時間や使用メモリもわかります。まあよくやったよ、うん
https://beta.atcoder.jp/contests/arc099/submissions?f.Task=&f.Language=&f.Status=&f.User=nuekodory